『効果検証入門』がアプリケーション開発エンジニアにとって得る物が多い本だった

読みました。アプリケーション開発エンジニア視点で読んで同僚に勧められる素晴しい内容でした。本稿はエンジニア視点のレビューになります。

効果検証入門〜正しい比較のための因果推論／計量経済学の基礎
技術評論社 (2019/1/18)
安井 翔太 (著), 株式会社ホクソエム (監修)
Kindle版/紙版両方あり

目次と構成

序 嘘っぱちの効果とそれを見抜けないデータ分析

1章 セレクションバイアスとRCT

2章 介入効果を測るための回帰分析

3章 傾向スコアを用いた分析

4章 差分の差分法（DID）とCausalImpact

5章 回帰不連続デザイン（RDD）

付録 RとRStudioの基礎
終 因果推論をビジネスにするために

まず効果検証とは何かという導入と共にビジネスの現場でありがちな誤りのある検証について解説があります。この誤りの原因となるセレクションバイアスと理想的な比較方法であるランダム化比較試験が1章です。以後の章はランダム化比較試験ができない状況において効果検証にどう取り組むか主要なアプローチ毎の手法の解説と実践例があります。

1章 セレクションバイアスとRCTより

想定読者は「効果検証を行なう必要のあるエンジニアやデータサイエンティスト」となっているのでバリバリ手を動かしてコードが書ける人が対象なのでしょう。文中の操作は全てRのコードが付いています。私はRがわからないのでPythonで再実装しつつ読み進めました。

どんな視点で読んだか

まず私はプロダクト開発エンジニアで、説明のためのモデルよりも予測のためのモデルを作る事が多く、Rはほぼ使った事がなく普段はPythonを書く人間です。機能リリース後の効果検証は解釈の容易さから主にランダム化比較試験を採用しますが、稀に適切なランダム割り当てができないケースで観察研究に頼る事があります。

良かった点

予測のためのモデル(機械学習)に慣れ親しんだ人間が持つ疑問に答えている

機械学習エンジニアは因果推論・計量経済学で用いられる線形回帰モデルよりも予測と汎化性能を重視したより複雑なモデルを扱います。なので当然「クロスバリデーションしなくていいのか?」とか「対数変換やスケーリングした方が精度が出るのでは?」と思うわけです。この様な予測をメインにしている人が効果検証における線形回帰モデルを見た時の違和感の解説が2章の終りにあります。

正しい比較が何の役に立つのか言及している

正確な効果検証が価値を生むビジネスケースとそうでないケースが挙げられています。因果推論で価値を生めるかどうかはビジネスの構造に依存するというのは実務者が持っておいて損がない心構えでしょう。最終章に

もし因果推論でビジネスに対する価値を発揮したいのであれば、「正しい情報がビジネスの価値になる」という構造を持っている環境へ移るか、もしくはそのような環境を作ることを強くお勧めします。

と記述があります。エンジニアは正に「正しい情報が価値を生む」側でしょう。私の現場では「機能開発すべきかどうかの事前調査」と「リリース後の効果検証」が因果推論が絡むタスクです。事前調査は「変数xがyに寄与しているならxを利用した機能開発を検討する」といった物で、これを見誤ると意味の無い機能を作ってしまいます。

説明モデルの作り方の参考としても若手に勧められる

新卒エンジニアが部署に配属される時期ですが、エンジニアはコンピューターサイエンス・機械学習よりのスキルを持つ事が多く。極端な例では「ディープラーニングは判るけど一般化線形モデルは知らない」といった事もあります。ただ実務では効果検証のために線形モデルを利用する事はあるので線形モデルの応用や説明モデルの作り方といった計量経済学寄りの知識も持って欲しい訳です。現場のエンジニアに計量経済学の入口として渡すのもアリかなと思いました。

分析コードの難しさがわかる

私は書籍中のR実装をPythonで書き直しながら読み進めましたが、OLSで線形モデルをフィットして係数を求める所までは簡単に再現ができましたが。そこから先のマッチングやIPWとなると途端に同じ結果を出すのが難しくなりました。本の結果という正解がある状況なので自分の仕込んだバグに気づけましたが、正解が無い状況ではコードがバグっているのか仮説が間違っていて期待通りの結果にならなかったのか見極めが非常に難しい事に気づかされます。バグが無くとも利用するライブラリを変えるとまた結果が変わります。

ただ「傾向スコアマッチングをした時には共変量のバランスを確認する」等の因果推論の手法が機能しているかどうかの確認ポイントと前提とする仮定がしっかり解説されており、各手法は知っていても実際に手を動かした事がない人のガイドになる内容になっています。

疑問が残った点

対数を用いた回帰分析 (2.4.3節) で、目的変数の対数を取った時の係数βが 0.1であれば10%引き上げると解釈できるとあったので手元で実験してみたが上手くいかなかった。xが1増える毎にyが倍(100%増)になるようなデータで係数βを求めても1にならないので、βが小さい時のみこの解釈ができる等の制約がありそう。この現象について教えて頂いたので最後に追記ました。

標準化平均差(Average Standardized Absolute Mean distance: ASAM)の定義がわからなかった。本文では「平均の差をその標準誤差で割った値」とあるが、標準誤差はサンプルサイズが増えた時にゼロに近づくのでASAMが発散してしまう気がした。ASAMを利用している論文はいくつも見つかるが定義そのものの数式がなかなか見つからない。平均の差を全標本の標準偏差で割った値が正解?

本だけでわからなかった点ですが、formula定義に出てくる I(re74^2) の I() が何かわからなかったのでRのドキュメントを調べました。混乱を避けるためのただの括弧みたいですね。

まとめ

以前からお世話になっている安井さんが実務者向けの因果推論の本を上梓されたとの事で非常に興味があったのですが、期待を裏切らない内容でした。安井さんは5年程前に予測性能に重きを置く機械学習と説明に重きを置くための因果推論・計量経済学の違いを教えてくれた方であり、それで自分の視野が一気に広がった経緯があります。なので若干バイアスのかかったレビューになっている事はご容赦ください。

因果推論は以前から興味があったもののRCT以外はほぼ使った事がなかったので、実務で利用する際の手順や注意点は非常に参考になりました。あとRが凄いので分析業務は素直にRを使おうという気持ちになりました。

追記

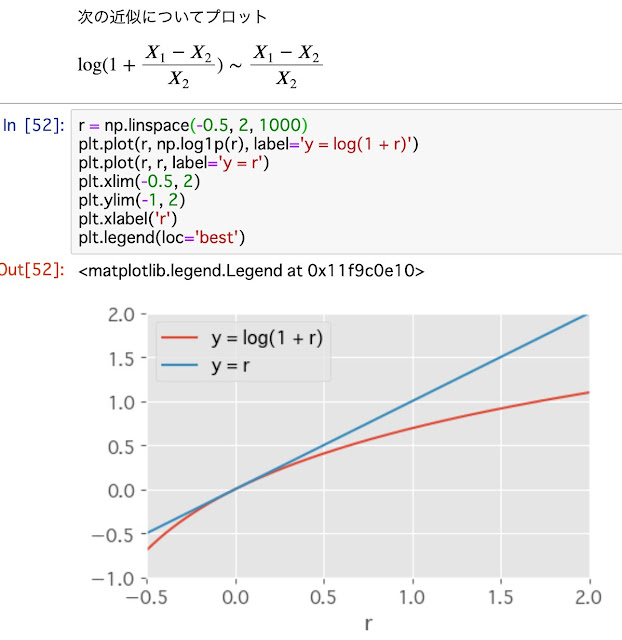
係数を解釈する時に利用している近似はマクローリン展開だから、ゼロから離れると二次以降の項が無視できなくなってズレが大きくなると教えてもらいました。プロットするとこうなります。